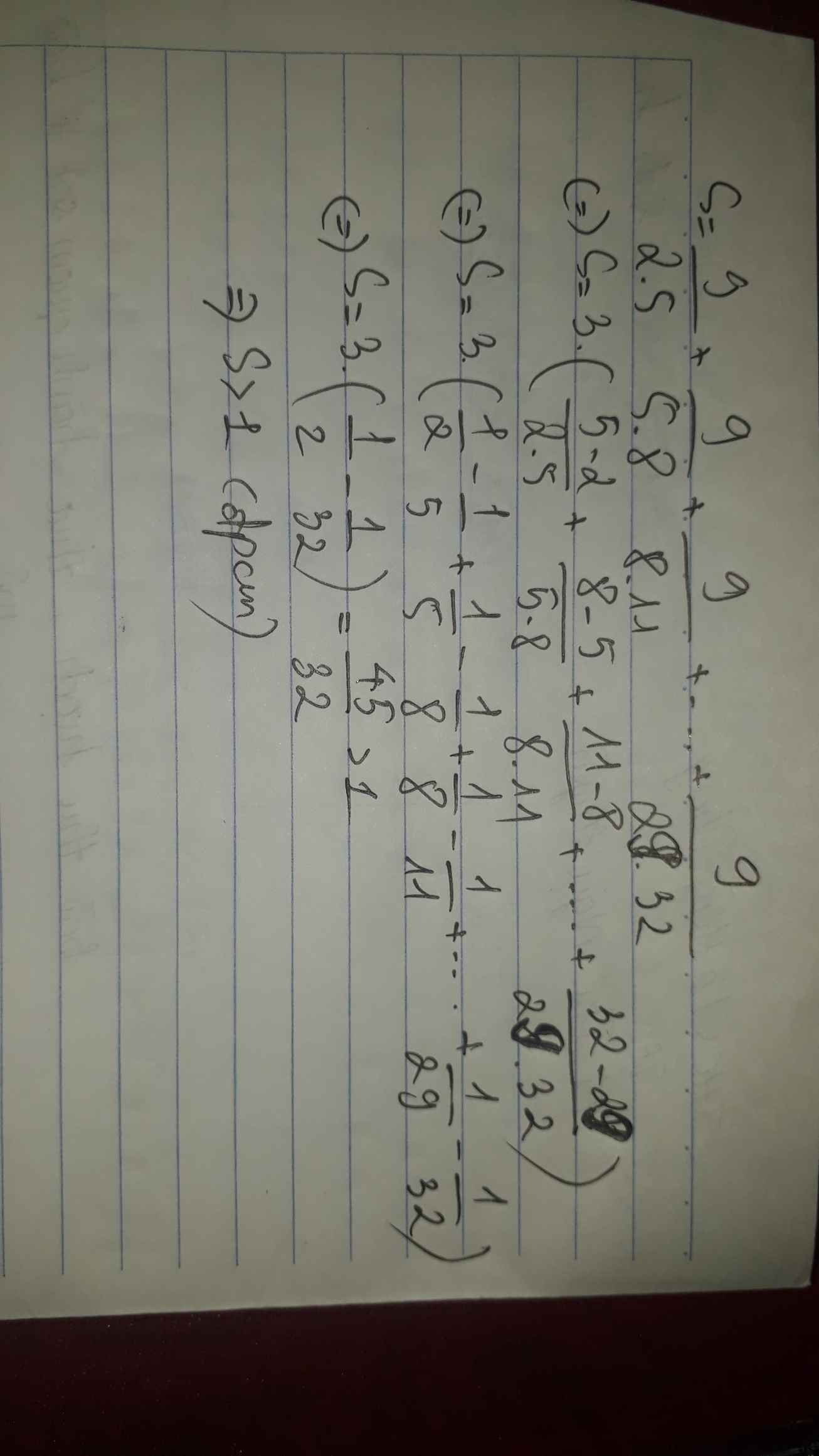Question

cho S= 9 phần 2.5+9 phần 5. 8 + 9 phần 8.11+..+9 phần 29.32. CM S>1

Answer 1

Answer 2

Ta có: 9/2.5  + 9/5.8 + 9/9.11+...+ 9/29.32

      =>9.(1/2 -1/5 + 1/5 - 1/8 +...+1/29 -1/32)

      =>9.( 1/2 -1/32)

      =>9. 15/32

      =>45/32 

Suy ra 45/32 >1 nên S>1

Answer 3

Ta có: \(S=\dfrac{9}{2\cdot5}+\dfrac{9}{5\cdot8}+\dfrac{9}{8\cdot11}+...+\dfrac{9}{29\cdot32}\)

\(=3\left(\dfrac{3}{2\cdot5}+\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+...+\dfrac{3}{29\cdot32}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{29}-\dfrac{1}{32}\right)\)

\(=3\left(\dfrac{1}{2}-\dfrac{1}{32}\right)\)

\(=3\cdot\dfrac{15}{32}=\dfrac{45}{32}>1\)