Question

Cho (O;R) và M nằm ngoài O vẽ 2 tiếp tuyến MA,MB . I là tiếp điểm MA,BI cắt O tại C A) Cm OAMB nội tiếp B) IA^2 = IB.IC C) Cm góc CMA = IBM

Answer 1

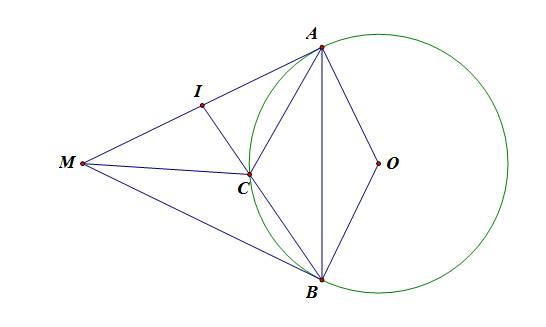
a, Vì MA, MB là tiếp tuyến của (O) nên \(\angle MAO=\angle MBO=90^o\)

Suy ra: tứ giác OAMB nội tiếp

b, Xét ΔIAC và ΔIBA, có: ∠I chung, \(\angle IAC=\angle IBA\)

\(\Rightarrow \Delta IAC\sim \Delta IBA(g.g) \Rightarrow \dfrac{IA}{IC}=\dfrac{IB}{IA} \Rightarrow IA^2=IB.IC\)

c, Vì I là trung điểm MA nên \(IM^2=IA^2=IB.IC\Rightarrow \dfrac{IC}{IM}=\dfrac{IM}{IB} \)

\(\Rightarrow \Delta ICM \sim \Delta IMB (c.g.c) \Rightarrow \angle IMC=\angle IBM \) hay \(\angle CMA=\angle IBM\)

Answer 2

a: góc OAM+góc OBM=180 độ

=>OAMB nội tiếp

b: Xet ΔIAC và ΔIBA có

góc IAC=góc IBA

góc AIC chung

=>ΔIAC đồng dạng với ΔIBA

=>IA^2=IB*IC