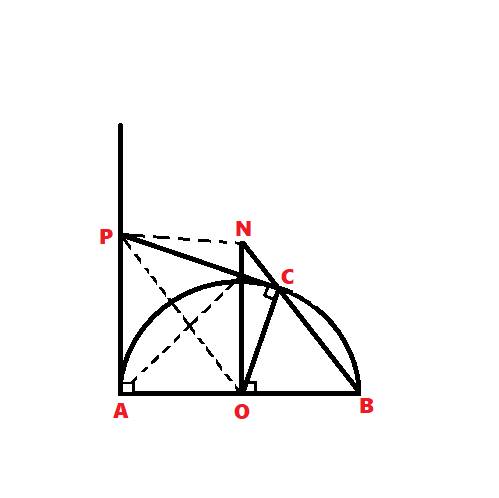
a:
Sửa đề: Chứng minh PO//NB
Xét (O) có
PA,PC là tiếp tuyến
Do đó: PA=PC
=>P nằm trên đường trung trực của AC(1)
OA=OC
=>O nằm trên trung trực của AC(2)
Từ (1) và (2) suy ra OP là đường trung trực của AC
=>OP\(\perp\)AC(3)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB(4)
Từ (3) và (4) suy ra CB//OP
b: NO\(\perp\)AB
AP\(\perp\)AB
Do đó: NO//AP
Xét ΔPAO vuông tại A và ΔNOB vuông tại O có
AO=OB
\(\widehat{POA}=\widehat{NBO}\)(hai góc đồng vị, PO//NB)
Do đó: ΔPAO=ΔNOB
=>PA=NO
Xét tứ giác PAON có
PA//NO
PA=NO
Do đó: PAON là hình bình hành
=>PN=OA
PN=OA
OA=OB
Do đó: PN=OB
PAON là hình bình hành
=>PN//OA
mà A\(\in\)OB
nên PN//OB
Xét tứ giác PNBO có
PN//OB
PO//NB
Do đó: PNBO là hình bình hành