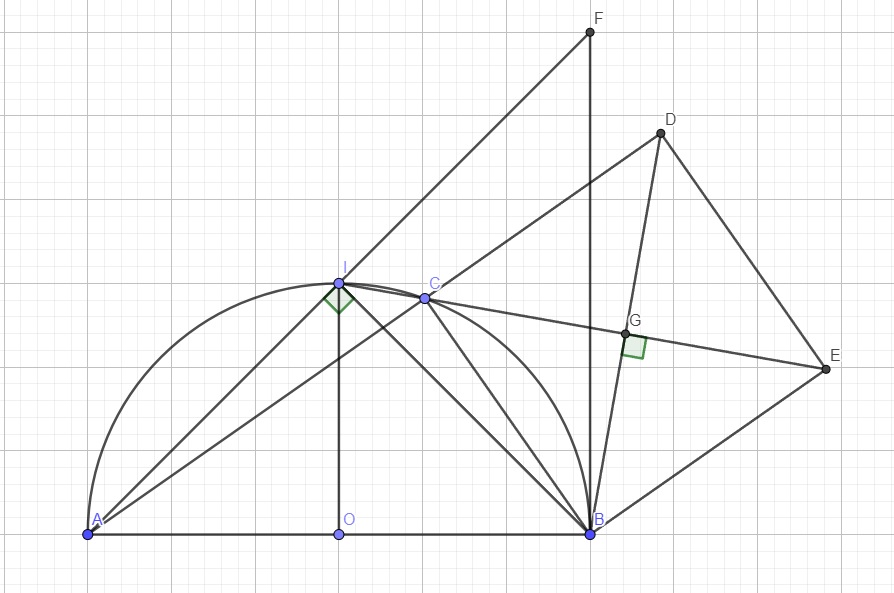
b.
Gọi I là điểm chính giữa cung AB \(\Rightarrow I\) cố định
Đồng thời ta có \(IA=IB\Rightarrow\Delta IAB\) vuông cân tại I
\(\Rightarrow\widehat{BAI}=45^0\)
Qua B kẻ đường thẳng vuông góc AB cắt AI kéo dài tại F \(\Rightarrow F\) cố định
Tam giác ABF vuông cân tại B (tam giác vuông có 1 góc \(\widehat{BAI}=45^0\))
\(\Rightarrow\widehat{AFB}=45^0\)
Đồng thời suy ra 3 điểm A,B,F thuộc đường tròn tâm I bán kính AI cố định.
\(BCDE\) là hình vuông \(\Rightarrow\widehat{CDB}=45^0\Rightarrow\widehat{AFB}=\widehat{ADB}=45^0\)
Lại có F, D nằm cùng 1 phía nửa mặt phẳng bờ AB
\(\Rightarrow AFDB\) nội tiếp (2 góc bằng nhau cùng chắn AB)
\(\Rightarrow D\) thuộc đường tròn (I;IA) cố định khi C di động
c.
Do F thuộc (I;IA) \(\Rightarrow IB=ID\Rightarrow I\) thuộc trung trực của BD
Mà ABCD là hình vuông \(\Rightarrow AC\) là trung trực của BD
\(\Rightarrow I\in AC\)
Vậy CE luôn đi qua điểm I cố định
d.
\(\widehat{CEB}=45^0\) (BCDE là hình vuông), mà I, C, E thẳng hàng theo cmt
\(\Rightarrow\widehat{IEB}=\widehat{IFB}=45^0\)
Lại có E, F nằm cùng phía nửa mặt phẳng bờ IB
\(\Rightarrow EBIF\) nội tiếp
\(\Rightarrow E\) thuộc đường tròn ngoại tiếp tam giác IBF cố định
e.
Gọi G là tâm hình vuông \(\Rightarrow BD\) và CE vuông góc nhau tại G
\(\Rightarrow\widehat{CGB}=90^0\)
Do I, C, E thẳng hàng \(\Rightarrow\widehat{IGB}=90^0\)
\(\Rightarrow G\) thuộc đường tròn đường kính IB cố định