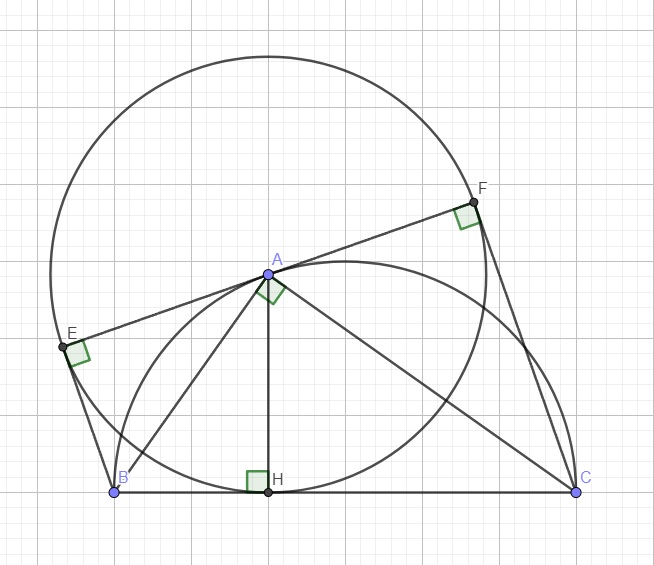
BC vuông góc AH tại H \(\Rightarrow BC\) là tiếp tuyến \(\left(A;AH\right)\) tại H
\(\Rightarrow B\) là giao điểm 2 tiếp tuyến của \(\left(A;AH\right)\) tại H và tại E
\(\Rightarrow BH=BE\)
Mà \(AH=AE\) (cùng là bán kính của \(\left(A;AH\right)\))
\(\Rightarrow AB\) là trung trực của EH
\(\Rightarrow AB\) đồng thời là phân giác \(\widehat{HAE}\) hay \(\widehat{HAB}=\widehat{EAB}\) (1)
Tương tự ta có AC là trung trực HF \(\Rightarrow\widehat{HAC}=\widehat{FAC}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\widehat{EAB}+\widehat{BAH}+\widehat{HAC}+\widehat{CAF}=2\left(\widehat{BAH}+\widehat{CAH}\right)\)
\(\Rightarrow\widehat{EAF}=2\widehat{BAC}\)
Trong (O), BC là đường kính nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow\widehat{EAF}=180^0\) hay 3 điểm E, A, F thẳng hàng
\(\Rightarrow BE||CF\) (cùng vuông góc EF)