Cho nửa đường tròn (O) đường kính AB. Điểm C thuộc (O) sao cho CA < CB. Vói H là hình chiếu vuông góc của C trên AB, gọi D, M, N theo thứ tự là giao của đường tròn I đường kính CH với (O), AC và BC
a, Tứ giác CMHN là hình gì?
b, Chứng minh OC ⊥ MN
c, Với E = AB ∩ CD, chứng minh các điểm E, I, M và N thẳng hàng
d, Chứng minh ED.EC = EA.EB
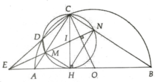
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm

