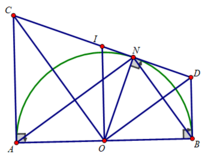
a)Ta có: DN và DB là hai tiếp tuyến cắt nhau tại D ⇒ DN = DB
CA và CN là hai tiếp tuyến cắt nhau tại C ⇒ CA = CN
Khi đó: DB + CA = DN + CN = DC
Mặt khác OC và OD lần lượt là hai phân giác của hai góc ∠(AON) và ∠(BON) kề bù nên
∠(COD) = 90 0
Trong tam giác vuông COD có ON là đường cao nên:
DN.CN = ON 2 = R 2
Hay AC.BD = R 2 (không đổi)

