Các câu hỏi tương tự
Cho hai khối nón (
N
1
),(
N
2
) . Chiều cao khối nón (
N
2
) bằng hai lần chiều cao khối nón (
N
1
) và đường sinh khối nón (
N
2
) bằng hai lần đường sinh khối nón (
N
1
). Gọi
V
1
,...
Đọc tiếp
Cho hai khối nón ( N 1 ),( N 2 ) . Chiều cao khối nón ( N 2 ) bằng hai lần chiều cao khối nón ( N 1 ) và đường sinh khối nón ( N 2 ) bằng hai lần đường sinh khối nón ( N 1 ). Gọi V 1 , V 2 lần lượt là thể tích hai khối nón ( N 1 ), ( N 2 ). Tỉ số bằng V 1 V 2
A. 1 6
B. 1 8
C. 1 16
D. 1 4
Cho dãy số
U
n
xác định bởi
U
n
1
n
3
4
+
n
3
+
3
n
2...
Đọc tiếp
Cho dãy số U n xác định bởi
U n = 1 n 3 4 + n 3 + 3 n 2 + 3 n + 1 4 1 n 3 + 2 n 2 + n 4 + n 3 + n 2 4 , n ≥ 1
Hãy tính tổng S = u 1 + u 2 + . . + u 2018 4 - 1
A. 2016
B. 2017
C. 2018
D. 2019
Cho hình nón
N
1
có chiều cao bằng 40cm. Người ta hình nón
N
1
bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ
N
2
có thể tích bằng
1
8
thể tích
N
1
. Tính chiều cao h của hình nón
N
2
A. 40cm. B. 10cm C. 20cm. ...
Đọc tiếp
Cho hình nón N 1 có chiều cao bằng 40cm. Người ta hình nón N 1 bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ N 2 có thể tích bằng 1 8 thể tích N 1 . Tính chiều cao h của hình nón N 2
A. 40cm.
B. 10cm
C. 20cm.
D. 5cm.
Cho hình nón
N
1
có chiều cao bằng 40cm. Người ta hình nón
N
1
bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ
N
2
có thể tích bằng
1
8
thể tích
N
1
. Tính chiều cao h của hình nón
N
2
A. 40 cm B. 10 cm C. 20 cm D. 5 cm
Đọc tiếp
Cho hình nón N 1 có chiều cao bằng 40cm. Người ta hình nón N 1 bằng một mặt phẳng song song với mặt đáy của nó để được một hình nón nhỏ N 2 có thể tích bằng 1 8 thể tích N 1 . Tính chiều cao h của hình nón N 2
A. 40 cm
B. 10 cm
C. 20 cm
D. 5 cm
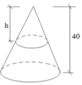
Một vật N1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N1 bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ N2 có thể tích bằng
1
8
thể tích N2.Tính chiều cao h của hình nón N2? A. 10cm B. 20cm C. 40cm D. 5cm
Đọc tiếp
Một vật N1 có dạng hình nón có chiều cao bằng 40cm. Người ta cắt vật N1 bằng một mặt cắt song song với mặt đáy của nó để được một hình nón nhỏ N2 có thể tích bằng 1 8 thể tích N2.Tính chiều cao h của hình nón N2?
A. 10cm
B. 20cm
C. 40cm
D. 5cm
Cho dãy số
u
n
như sau :
u
n
:
n
1
+
n
2
+
n
4
,...
Đọc tiếp
Cho dãy số u n như sau : u n : n 1 + n 2 + n 4 , ∀ n = 1 , 2 , . . . Tính giới hạn l i m n → + ∞ u 1 + u 2 + . . . + u n
A. 1 4
B. 1
C. 1 2
D. 1 3
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đâyCách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón
N
1
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón
N
2
Gọi
V
1
,
V
2...
Đọc tiếp
Từ một hình tròn có tâm S, bán kính R, người ta tạo ra các hình nón theo hai cách sau đây
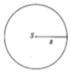
Cách 1: Cắt bỏ 1/4 hình nón rồi ghép hai mép lại được hình nón N 1
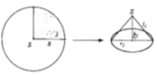
Cách 2: Cắt bỏ 1/2 hình nón rồi ghép hai mép lại được hình nón N 2
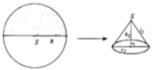
Gọi V 1 , V 2 lần lượt là thể tích của khối nón N 1 và khối nón N 2 . Tính V 1 V 2
A. V 1 V 2 = 9 3 4 2
B. V 1 V 2 = 3 3 2 2
C. V 1 V 2 = 7 2 3
D. V 1 V 2 = 9 7 8 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
P
)
:
(
1
-
m
2
)
2
n
x
+
4
m
n
y
+
(
1
+
m
2
)
(
1
-
n
2
)
z
+
4
(
m...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : ( 1 - m 2 ) 2 n x + 4 m n y + ( 1 + m 2 ) ( 1 - n 2 ) z + 4 ( m 2 + n 2 + m 2 n 2 + 1 ) = 0 Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là:
A. 1
B. 2
C. 3
D. 4
Hàm số
y
x
+
m
3
+
x
+
n
3
−
x
3
(tham số m, n) đồng biến trên khoảng
−
∞
;
+
∞
.
Giá trị n...
Đọc tiếp
Hàm số y = x + m 3 + x + n 3 − x 3 (tham số m, n) đồng biến trên khoảng − ∞ ; + ∞ . Giá trị nhỏ nhất của biểu thức P = 4 m 2 + n 2 − m − n bằng
A. -16
B. 4
C. − 1 16
D. 1 4
Chứng tỏ rằng nếu phân số $\frac{7n^2+1}{6}$7n2+16 là số tự nhiên với n thuộc N thì các phân số $\frac{n}{2}$n2 và $\frac{n}{3}$n3 là các phân số tối giản
