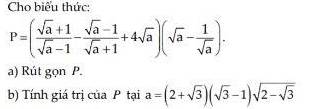Question

cho mình hỏi câu 5.1.7 với ạ

 

Answer 1

5.1.7

\(\Delta'=m^2-\left(-2m-1\right)=\left(m+1\right)^2>0\Rightarrow m\ne-1\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=-2m-1\end{matrix}\right.\)

Để biểu thức đề bài xác định \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2m\ge0\\3+x_1x_2=2-2m\ge0\end{matrix}\right.\)

\(\Rightarrow0\le m\le1\)

Khi đó ta có:

\(\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1\)

\(\Leftrightarrow\sqrt{2m}+\sqrt{2-2m}=2m+1\)

\(\Leftrightarrow\sqrt{2m}-1+\sqrt{2-2m}-1=2m-1\)

\(\Leftrightarrow\dfrac{2m-1}{\sqrt{2m}+1}+\dfrac{1-2m}{\sqrt{2-2m}+1}=2m-1\)

\(\Leftrightarrow\left(2m-1\right)\left(1+\dfrac{1}{\sqrt{2-2m}+1}-\dfrac{1}{\sqrt{2m}+1}\right)=0\)

\(\Leftrightarrow\left(2m-1\right)\left(\dfrac{\sqrt{2m}}{\sqrt{2m}+1}+\dfrac{1}{\sqrt{2-2m}+1}\right)=0\)

\(\Leftrightarrow2m-1=0\) (do \(\dfrac{\sqrt{2m}}{\sqrt{2m}+1}+\dfrac{1}{\sqrt{2-2m}+1}>0;\forall m\in TXĐ\))

\(\Rightarrow m=\dfrac{1}{2}\) (thỏa mãn)