Đáp án C.
Phương pháp
So sánh diện tích đáy và chiều cao của các khối chóp.
Cách giải
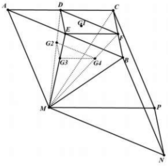
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì G 2 ; G 3 ; G 4 là trọng tâm các tam giác MAC, MAB, MBC nên
G 2 ∈ M D ; M G 2 = 2 D G 2 G 3 ∈ M E ; M G 3 = 2 E G 3 G 4 ∈ M F ; M G 4 = 2 F G 4 ⇒ G 2 G 3 G 4 / / D E F ⇒ V 1 = V E . G 2 G 3 G 4 = F G 3 M G 3 . V M . G 2 G 3 G 4 = 1 2 V M . G 2 G 3 G 4
Lại có
V M . G 2 G 3 G 4 V M D E F = M G 2 . M G 3 . M G 4 M D . M E . M F = 2 3 . 2 3 . 2 3 = 8 27
⇒ V 1 = 1 2 8 27 V M D E F = 4 27 V M D E F
Lại có
S D E F = 1 4 S A B C ⇒ V M . D E F = 1 4 V M . A B C = 1 4 . 1 3 V = 1 12 V
Vậy
V 1 = 4 27 . V 12 = V 81