Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là
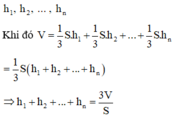
Đáp án D
Gọi O là một điểm bất kì bên trong khối đa diện.
Chia khối đa diện đều n mặt đã cho thành n khối chóp có đỉnh là O và các mặt đáy là các mặt của khối đa diện. Chiều cao hạ từ O đến n mặt tương ứng là
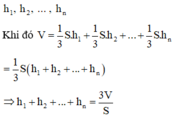
Cho khối đa diện đều n mặt có thể tích là V và diện tích mỗi mặt của nó là S. Khi đó tổng khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng
A. 3 V S
B. V nS
C. nV S
D. 3 S V
Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó, tổng các khoảng cách từ một điểm bất kỳ bên trong khối đa diện đó đến các mặt bên bằng
A. V 3 S
B. n V S
C. 3 V S
D. V n S
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, và SA vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 45 ° . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 khối đa diện còn lại có thể tích V 2 (tham khảo hình vẽ bên đây). Tính tỉ số V 1 V 2
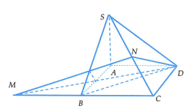
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, B A D ^ = 60 ° và SA vuông góc với mặt phẳng (ABCD). Góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 450. Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng (MND) chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V1, khối đa diện còn lại có thể tích V2 (tham khảo hình vẽ bên). Tính tỉ số V 1 V 2

A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , B A D ⏜ = 60 0 và SA vuông góc với mặt phẳng A B C D . Góc giữa hai mặt phẳng S B D và A B C D bằng 45 0 . Gọi M là điểm đối xứng của C qua B và N là trung điểm của SC. Mặt phẳng M N D chia khối chóp S.ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích V 1 và khối đa diện còn lại có thể tích bằng V 2 . Tính tỉ số V 1 V 2
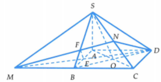
A. V 1 V 2 = 12 7
B. V 1 V 2 = 5 3
C. V 1 V 2 = 1 5
D. V 1 V 2 = 7 5
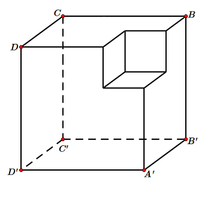
Một khối đa diện (H) được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ. Gọi (S) là khối cầu có thể tích lớn nhất chứa trong (H) và tiếp xúc với các mặt (A'B'C'D'),(BCC'B'),(DCC'D'). Tính bán kính của (S).
A. 2 + 3 3
B. 3 - 3
C. 2 3 3
D. 2
Một hình lập phương có diện tích mặt chéo bằng a 2 2 . Gọi V là thể tích khối cầu và S là diện tích mặt cầu ngoại tiếp hình lập phương nói trên. Khi đó tích S.V bằng
A. S V = 3 π 2 a 5 2
B. S V = 3 3 π 2 a 5 2
C. S V = 3 6 π 2 a 5 2
D. S V = 3 π 2 a 5 2