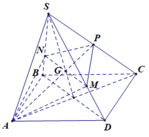
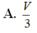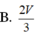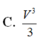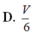Phương pháp:
Tìm giao điểm C' của SC với (AB'D')
Tính tỉ số S C ' S C
Sử dụng công thức tỉ số thể tích đối với khối chóp tam giác để tính toán.
Cách giải:
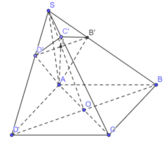
Gọi O là tâm của hình bình hành ABCD. SO cắt B'D' tại I.
Nối AI cắt SC tại C' nên A, B', C', D' đồng phẳng
Đặt ![]()
Ta có: 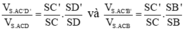
Do đó: 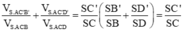
Hay 
![]()
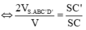
![]()
Xét tam giác ∆ SCO có C', I, A thẳng hàng nên áp dụng định lý Me – ne – la – uýt ta có:
![]()
![]()
Vậy ![]()
![]()
Hay tỷ số thể tích của hai khối đa diện được chia ra bởi (AB'D') là:
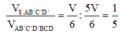
Chọn D.