Đáp án C
Cách 1: Giải bằng hàm số
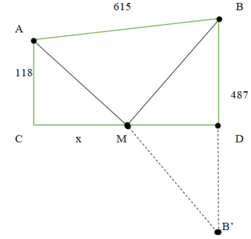
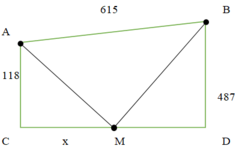
Đặt CM = x (x > 0)
Dễ tính ra CD = 615 2 - ( 487 - 118 ) 2 = 492
Từ đề bài ta có: f(x) = x 2 + 118 2 + ( 492 - x ) 2 + 487 2
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = - 2 x 2 x 2 + 118 2 + 2 ( 492 - x ) 2 ( 492 - x ) 2 + 487 2
⇒ f’(x) = 0
⇔ ( 492 - x ) x 2 + 118 2 - x ( 492 - x ) 2 + 487 2 = 0
⇔ ( 492 - x ) 2 ( x 2 + 118 2 ) - x 2 ( ( 492 - x ) 2 + 487 2 ) = 0
⇔ x = 58056 605
Ta có bảng biến thiên
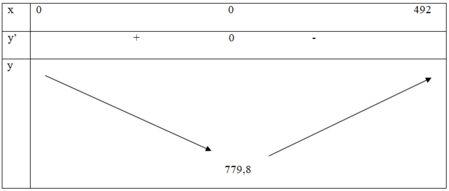
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇒ AM + MB ngắn nhất
⇒ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
=>AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng