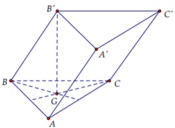
Đáp án A.
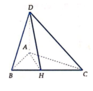
Từ dữ liệu đề bài ta thấy A B 2 + A C 2 = B C 2 ⇒ tam giác ABC vuông tại A.
Trong mặt phẳng A B C kẻ A H ⊥ B C tại H.
Ta có D A ⊥ B C A H ⊥ B C D A ∈ D A H ; A H ∈ D A H D A ∩ A H = A ⇒ D H ⊥ B C (định lý ba đường vuông góc).
Ta có A B C ∩ D B C = B C A H ⊥ B C ; D H ⊥ B C A H ∈ A B C ; D H ∈ D B C ⇒ A B C , D B C ^ = A H D ^ .
Ta có A H = A B . A C B C = 3 a .4 a 5 a = 12 a 5 .
Tam giác ADH vuông tại A.
⇒ tan A H D ^ = D A A H = 3. V A B C D S A B C 12 a 5 = 3.24 3 a 3 15. 1 2 .3 a .4 a 12 a 5 = 3 3
⇒ A H D ^ = 30 °
Vậy ta chọn A.