Cho hình thoi ABCD có B A D ^ = 60 ° , A B = 2 a . Gọi H là trung điểm của AB. Trên đường thẳng d vuông góc với mặt phẳng (ABCD) tại H lấy điểm S thay đổi khác H. Trên tia đối của tia BC lấy điểm M sao cho B M = 1 4 B C . Tính theo a độ dài của SH để góc giữa SC và (SAD) có số đo lớn nhất
A. S H = 21 4 4 a .
B. S H = 21 4 4 a .
C. S H = 21 4 a .
D. S H = 21 4 a .
Đáp án A
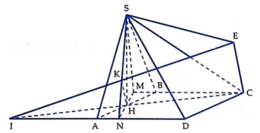
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2 3 a x 4 x 2 + 3 a 2 x 2 + 7 a 2
⇒ sin φ = 2 3 a x 4 x 4 + 21 a 4 + 31 a 2 x 2 ≤ 2 3 a x 4 21 a 2 x 2 + 31 a 2 x 2 = 2 3 4 21 + 31
Dấu “=” xảy ra khi và chỉ khi 4 x 4 = 21 a 4 ⇔ x 4 = 21 4 a 4 ⇔ x = 21 4 4 a .
Vậy góc φ đạt lớn nhất khi sin φ đạt lớn nhất, khi đó S H = 21 4 4 a