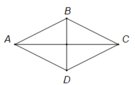
Từ giả thiết ta có tam giác ABD câ tại A và có 1 góc bằng 60.
suy ra tam giác ABD đều cạnh a nên
Đúng 0
Bình luận (0)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
cho hình hộp chữ nhật ABCD, ABCD mệnh đề nào sau đây đúng?A) (ABCD) ⊥ (ABB A).B) (ABCD) ⊥ (A BD).C. (ABB A) ⊥ (CDDC).D. (ABCD) ⊥ (ABCD).
Đọc tiếp
cho hình hộp chữ nhật ABCD, A'B'C'D' mệnh đề nào sau đây đúng?
A) (ABCD) ⊥ (ABB ' A').
B) (ABCD) ⊥ (A' BD).
C. (ABB' A') ⊥ (CDD'C').
D. (ABCD) ⊥ (A'B'C'D').
Cho hình lăng trụ đứng ABCD. D có ABCD là hình thoi cạnh a, góc giữa đường thẳng A B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B D
Đọc tiếp
Cho hình lăng trụ đứng ABCD. 'D ' có ABCD là hình thoi cạnh a, góc giữa đường thẳng A 'B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B ' D '
LV
27 tháng 4 2021 lúc 19:30
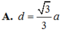
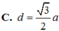
Cho hình chóp SABCD đáy là hình vuông tâm O cạnh a. SA=a căn 3. SA vuông góc với đáy. Tính góc a)(SBD) và (ABCD) b)(SBD) và (SAB) c)(SBC) và (ABCD) d)(SCD) và (ABCD)
Bài 10. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, cạnh bên bằng a * sqrt(3) . O là tâm hình vuông 1/ Chứng minh :a) (SAC) I (ABCD) b) (SAC) (SBD). 2 / a ) Tính d(S; (ABCD)) b) Tính d(O; (SCD)) 3/ Tính góc giữa:a) SC và (ABCD); b) (SAB) và (ABCD).
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A, B, C, D.a) Tứ giác A, B, C, D là hình gì? Chứng minh rằng .b) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).c) Chứng minh rằng điều kiện để tứ giác A, B, C, D là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Đọc tiếp
Trên mặt phẳng (α) cho hình vuông ABCD. Các tia Ax, By, Cz, Dt vuông góc với mặt phẳng (α) và nằm về một phía đối với mặt phẳng (α). Một mặt phẳng (β) lần lượt cắt Ax, By, Cz, Dt tại A', B', C', D'.
a) Tứ giác A', B', C', D' là hình gì? Chứng minh rằng .
b) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình thoi là nó có hai đỉnh đối diện cách đều mặt phẳng (α).
c) Chứng minh rằng điều kiện để tứ giác A', B', C', D' là hình chữ nhật là nó có hai đỉnh kề nhau cách đều mặt phẳng (α).
Cho hình vuông ABCD (các đỉnh hình vuông ghi theo chiều ngươ chiều kim đồng hồ) có tâm O. Phép quay tâm O với góc quay nào dưới đây biến điểm A thành điểm C ? A. 90 B.45 C. -90 D.180
Cho hình chóp S.ABCD có ABCD là hình vuông tâm O, cạnh a SA vuông góc với mặt phẳng (ABCD) và SA=a căn 2. Tính khoảng cách từ:
a) C đến mặt phẳng (SAB).
b) từ A đến (SCD).
c) Từ O đến (SCD).
d) Khoảng cách giữa hai đường thẳng AB và SC.
Phần I: Trắc nghiệmCho hình chóp S.ABCD có đáy ABCD là hình bình hành. - Đặt
S
A
→
a
→
,
S
B
→
b
→
,
S
C
→
c
→
,
S
D
→
d...
Đọc tiếp
Phần I: Trắc nghiệm
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành.
- Đặt S A → = a → , S B → = b → , S C → = c → , S D → = d → .Khẳng định nào sau đây đúng?
A. a → + c → = d → + b →
B. a → + b → = d → + c →
C. a → + d → = b → + c →
D. a → + b → + c → + d → = 0 →
LV
18 tháng 5 2021 lúc 9:25
Cho hình chóp SABCD. ABCD là hình thoi tâm Ở cạnh a. Góc BAD=60°. SO vuông góc với (ABCD). Góc giữa SC và đáy bằng 60°. Tính khoảng cách a)O đến (SBC) b)A đến (SBC) c)AD đến (SCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SASBSCSDa√2; O là tâm của hình vuông ABCD.a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD). b) C/m (SAC) ⊥(SBD)c) Tính khoảg cách từ S đến (ABCD)d) Tính góc giữa đường SB và (ABCD).e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCDf) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)g) Tính khoảng cách giữa SM và BC; SM và AB.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.