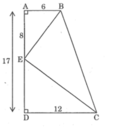
Ta có: AD = AE + DE
Suy ra: DE = AD – AE = 17 – 8 = 9cm
Xét △ ABE và △ DEC, ta có:
∠ A = ∠ D = 90 0 (1)
Mà :
Suy ra: 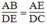 (2)
(2)
Từ (1) và (2) suy ra : △ ABE đồng dạng △ DEC (c.g.c)
Suy ra: ∠ ABE = ∠ DEC
Trong △ ABE ta có: ∠ A = 90 0 ⇒ ∠ (AEB) + ∠ (ABE) = 90 0
Suy ra: ∠ (AEB) + ∠ (DEC) = 90 0
Lại có: ∠ (AEB) + ∠ (BEC) + ∠ (DEC) = 180 0 (kề bù)
Vậy : ∠ (BEC) = 180 0 - ( ∠ (AEB) + ∠ (DEC)) = 180 0 - 90 0 = 90 0