a, Do CD//AB, DM//BD nên ta dễ thấy: tam giác DMC đồng dạng với tam giác BCA(g.g)
➞ \(\frac{MC}{CA}=\frac{CD}{AB}=\frac{AF}{AB}\) ( vì ADCF là hình bình hành nên CD=AF) (1)
Ta lại có: FP//AC nên:\(\frac{CP}{CB}=\frac{AF}{AB}\) (2)
Từ (1),(2) ta có: \(\frac{CM}{CA}=\frac{CP}{CB}\)
Theo định lí Talet đảo ta có: MP//AB
b, Gọi N, N' là giao điểm của MP,DB với CF
Ta có:\(\frac{CN}{CF}=\frac{CM}{CA}=\frac{CD}{AB}\) ( theo phần a,)
\(\frac{CN'}{N'F}=\frac{CD}{FB}\)suy ra \(\frac{AN'}{CF}=\frac{CD}{\left(FB+CD\right)}=\frac{CD}{AB}\) ( vì CD=AF)
Vậy CN=CN' nên N' trùng N
Từ đó ta suy ra: MP,CF,DB đồng quy
Bài 2: Định lý đảo và hệ quả của định lý Talet
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho hình thang ABCD có đáy nhỏ CD. Từ D vẽ đường thẳng // với BC, cắt AC tại M, AB tại K. Từ C vẽ đường thẳng // với AD, cắt AB tại F. Từ F lại vẽ đường thẳng // với AC, cắt BC tại P. CMR:
a) MP//AB
b) 3 đường thẳng MP, CF, BD đồng quy
: Cho hình thang ABCD (AB < CD và AB // CD). Vẽ qua A đường thẳng AK song song với BC (K DC) và AK cắt BD tại E, vẽ qua B đường thẳng BI song song với AD (I CD) cắt AC tại F.
a) Chứng minh rằng: EF // AB
b) Chứng minh rằng: AB2 = CD.EF
Cho tứ giác ABCD, AC và BD cắt nhau tại O. Đường thẳng qua O và song song với BC cắt AB ở E; đường thẳng song song với CD qua O cắt AD tại F.
a) Chứng minh FE song song BD
b) Từ O kẻ các đường thẳng song song với AB, AD cắt BD, CD tại G và H. Chứng minh: CG.DH=BG.CH
Cho hình thang ABCD (AB // CD) có O là giao điểm của hai đường chéo AC và BD. Qua A, kẻ đường thẳng song song với BC cắt BD tại E. Qua B, kẻ đường thẳng song song với AD cắt AC tại F.
a) Chứng minh: EF // CD.
b) Chứng minh: AB2 = CD . EF
Cho tam giác ABC có O nằm trong tam giác. Đường thẳng qua O song song với BC cắt AB,AC tại M,N. Đường thẳng qua O song song với AB cắt AC, BC tại F, E. Đường thẳng qua O song song với AC cắt AB, BC tại I, K.
Chứng minh: \(\dfrac{AI}{AB}+\dfrac{BE}{BC}+\dfrac{CN}{AC}=1\)
Cho tứ giác ABCD. Qua E thuộc cạnh AD, kẻ đường thẳng song song với DC cắt AC tại G. Qua G kẻ đường thẳng song song CB cắt AB tại H. a. Chứng minh: HE song song BD. b. Qua B kẻ đường thẳng song song với CD cắt AC tại I. Qua C kẻ đường thẳng song song với BA cắt BA tại F. Chứng minh: IF song song AD.
Cho hình thang ABCD( AB//CD; AB<CD) . Hai đường chéo cắt
nhau tại O.
a) CMR: OA.OD=OB.OC
b) Đường thẳng đi qua O mà song song với CD cắt AD và BC lần lượt
tại M và N. CMR: OM=ON.
c) AD cắt BC tại E. EO cắt AB và CD lần lượt tại P và Q. CMR: P là
trung điểm của AB; Q là trung điểm của CD;
mg giúp mình câu c với
Cho hình thang ABCD (AB //CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q chứng minh 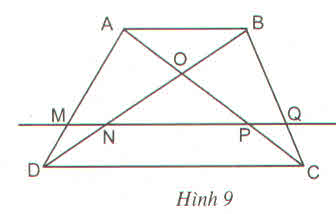 DN\BD=CP\AC
DN\BD=CP\AC
Cho DABC vuông tại A, đường phân giác của góc A cắt BC tại D biết AB = 6 cm , AC = 8 cm . a) Tính BC, BD, DC b) Từ trung điểm M của BC kẻ 1 đường thẳng song song với AD cắt cạnh AC tại F và cắt tia đối của tia AB tại E .Chứng minh: . c) Chứng minh: AE = AF
