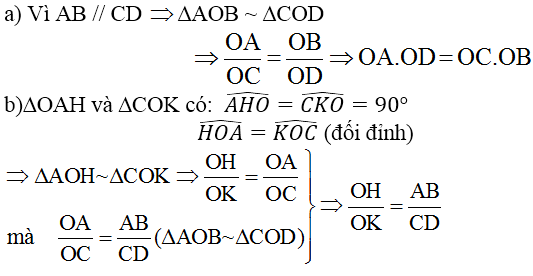
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)
Cho biểu thức \(P=10^{50}+5.10^{20}+1\) . Chứng minh rằng P không phải là bình phương của một số tự nhiên .
ai có thể cm \(\dfrac{OA}{AB}\)=\(\dfrac{OB}{BD}\) hông