Các câu hỏi tương tự
1,điểm O là giao điểm của các đường chéo của hình thang ABCD(AB song song với CD)biết diện tích tam giác AOB,COD theo thứ tự bằng a2,b2.tính diện tích hình thang
.Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự lần lượt là ở E và ở F. Chứng minh rằng OM = ON theo cách tính diện tích
Cho hình thang ABCD (AB//CD; AB<CD). Gọi O là giao của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB cắt AD, BC tại M,N
a, chứng minh OA.OD=OB.OC
b, biết AB=5cm; CD=10cm; OC=6cm. Tính OA,OM
c, chứng minh 1/OM = 1/ON = 1/AB + 1/ CD
Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của 2 đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự E và G. a) Chứng minh OA.OD=OB.OC. b) Cho AB = 5 cm, CD= 10 cm, Oc = 6 cm. Tính OA, OE. c) Chứng minh rằng : 1/OE = 1/OG = 1/AB + 1/CD ( giúp mik với ạ
Cho hình thang ABCD (AB//CD).gọi O là giao điểm 2 đường chéo.
a. Chứng minh rằng : OA.OD=OB.OC
b.Kẻ đường thẳng qua O và song song với CD cắt AD,BC lần lượt tại M và N.Chứng minh rằng: ON=OM.
Xem chi tiết
1. Cho tam giác đều ABC. Gọi M, N lần lượt là các điểm trên cạnh AB và BC sao cho BM BN. Gọi G là trọng tâm của tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác ICG2.Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự lần lượt là ở M và ở N. a. Chứng minh rằng OM ON b. Chứng minh rằng frac{1}{AB}+frac{1}{CD}frac{2}{MN} c. Biết SAOB 20082 ( đơn vị diện tích) ; SCOD20092 ( đơn vị diện...
Đọc tiếp
1. Cho tam giác đều ABC. Gọi M, N lần lượt là các điểm trên cạnh AB và BC sao cho BM = BN. Gọi G là trọng tâm của tam giác BMN và I là trung điểm của AN. Tính các góc của tam giác ICG
2.Hình thang ABCD (AB//CD) có hai đường chéo cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự lần lượt là ở M và ở N.
a. Chứng minh rằng OM = ON
b. Chứng minh rằng \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c. Biết SAOB= 20082 ( đơn vị diện tích) ; SCOD=20092 ( đơn vị diện tích ). Tinh SABCD.
Cho hình thang ABCD (AB//CD) có CD = 2AB. Gọi O là giao điểm của hai đường chéo AC và BD, F là giao điểm cạnh bên AD và BC
a) Chứng minh OC = 2OA
b) Điểm O là điểm đặc biệt gì trong tam giác FCD
c) Một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD, AC, BC tại M, I, K, N. Chứng minh DM/AD=CN/BC
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF
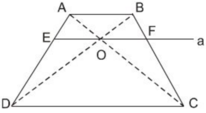
Bài 1: Cho hình thang ABCD ( AB // CD), đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với AB cắt các cạnh bên AD, BC lần lượt tại M, N.
1. Chứng minh: OM = ON 2. Chứng minh: (AM/AD)+(CN/CB)=1
