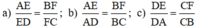Xét hình thang ABCD có EF//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BF}{FC}\)
=>\(\dfrac{ED}{AE}=\dfrac{CF}{FB}\)
=>\(\dfrac{ED+EA}{AE}=\dfrac{CF+FB}{FB}\)
=>\(\dfrac{AD}{AE}=\dfrac{BC}{FB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BF}{BC}\)
=>\(\dfrac{BF}{BC}=1-\dfrac{ED}{AD}\)
=>\(\dfrac{BF}{BC}+\dfrac{ED}{AD}=1\)