a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ
a: DN/BD=DM/DA
CP/CA=CQ/CB
mà DM/DA=CQ/CB
nên DN/BD=CP/CA
b: Xét ΔDAB có MN//AB
nên MN/AB=DM/DA
Xet ΔCAB có PQ//AB
nên PQ/AB=CQ/CP
mà DM/DA=CQ/CP
nên MN=PQ
Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC, và BC theo thứ tự các điểm M, N, P, Q. Chứng minh rằng MN = PQ.
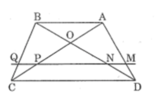
Cho hình thang ABCD (AB // CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD, BD, AC, và BC theo thứ tự các điểm M, N, P, Q. Chứng minh rằng MN = PQ.
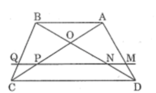
cho hình thang ABCD (AB//CD). Đường thẳng song song với đáy AB cắt các cạnh bên và các đường chéo AD,BD,AC và BC theo thứ tự tại các điểm M,N,P,Q.
CMR: MN=PQ
Lại làm phiền tới mấy bạn oy.......sorry....
Mấy bạn giúp mình với!!!! Thank you...
Hình thang ABCD (AB // CD) có hai đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
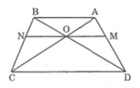
Cho hình thang ABCD (AB song2 CD). Đường thẳng song song với Ab cắt các cạnh bên và các đường chéo AD,BD,AC,BC thoe thứ tự M,,N,P,Q. CMR:MN=PQ
Cho hình thang ABCD, đáy AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và AB tại F. Đường thẳng qua E, song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại M
a, Chứng minh bốn điểm M,N,P,Q nằm trên 1 đường thẳng song song với hai đáy
b, Chứng minh: MN = PQ
c, Cho AB=a, CD=b. Chứng minh rằng các điểm M, N,P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, DC theo cùng 1 tỉ số k. Tính k theo a và b.
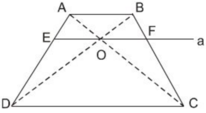
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F
Chứng minh rằng OE = OF.
Cho hình thang ABCD, đáy lớn là AB. Đường thẳng kẻ từ C song song với AD cắt đường chéo BD ở M, cắt AB ở F. Đường thẳng kẻ từ D song song với BC cắt đường chéo
AC ở N, cắt AB ở E. các đường thẳng kẻ từ E và F lần lượt song song với BD và AC cắt
AD và BC theo thứ tự ở P và Q. Chứng minh rằng 4 điểm M, N, P, Q thẳng hàng
Cho hình thang ABCD (AB // CD). Hai đường chéo AC và BD cắt nhau tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự tại E và F (h.26).
Chứng minh rằng OE = OF