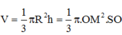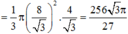Đáp án C
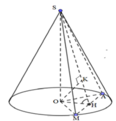
Phương pháp: Xác định góc giữa hai mặt phẳng α ; β :
- Tìm giao tuyến ∆ của α ; β
- Xác định 1 mặt phẳng γ ⊥ △
- Tìm các giao tuyến a = α ∩ γ , b = β ∩ γ
- Góc giữa hai mặt phẳng α ; β : α ; β = a;b
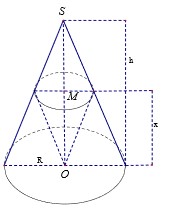
Cách giải: Kẻ OH ⊥ AM, H ∈ AM, OK ⊥ SH, K ∈ SH
Vì 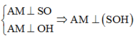
=> AM ⊥ OK
Mà OK ⊥ SH => OK ⊥ (SAM) => d(O;(SAM)) = OK = 2
Ta có: 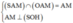 ( vì AM
⊥
OH, AM
⊥
SO)
( vì AM
⊥
OH, AM
⊥
SO)
Mà (SOH) ∩ (OAM) = OH; (SOH) ∩ (SAM) = SH => ((SAM);(OAM)) = (SH;OH) = S H O ^ = 30 0
Tam giác OHK vuông tại K
![]()
Tam giác SOH vuông tại O
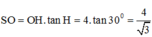
Tam giác OAM cân tại O, A O M ^ = 60 0 , OH ⊥ AM
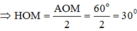
Tam giác OHM vuông tại H
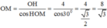
Thể tích khối nón: