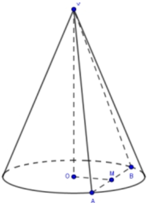
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 0 . Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh S x q của hình nón N .
A. S x q = 36 3 π .
B. S x q = 27 3 π .
C. S x q = 18 3 π .
D. S x q = 9 3 π .
Đáp án C.
Phương pháp:
Diện tích xung quanh của hình nón: S x q = π R l
Cách giải:
Gọi M là trung điểm AB ⇒ O M ⊥ A B . Mà O M ⊥ S O (vì SO vuông góc với đáy)
⇒ OM là đoạn vuông góc chung của SO và AB
⇒ d S O ; A B = O M = 3
Tam giác OMA vuông tại M:
O A 2 = O M 2 + M A 2 ⇒ R 2 = 3 2 + M A 2 ⇒ M A = R 2 − 9
Tam giác SAB vuông tại A có S A = S B (Vì Δ S O B = Δ S O A c . g . c )
⇒ Δ S A B vuông cân tại S
⇒ S A = A B 2 = 2 A M 2 = A M . 2 = 3 R 2 − 18
(N) có góc ở đỉnh là
120 0 ⇒ A S O = 60 0
Tam giác SOA vuông tại O:
sin O S A = O A S A ⇒ sin 60 0 = R 3 R 2 − 18 = 3 2 ⇒ 2 R = 3 . 3 R 2 − 18 ⇔ 4 R 2 = 6 R 2 − 54
⇔ R 2 = 27 ⇒ R = 3 3 .
l = S A = 2 R 2 − 18 = 2.27 − 18 = 36 = 6
S x q = π R l = π .3 3 .6 = 18 π 3