Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Suy luận: Cung AB ngược hướng dương của đường tròn lượng giác nên có số đo âm, còn DA và EA có số đo dương. Do đó các phương án A, C, D bị loại.
Đáp án: B
Một hình lục giác đều ABCDEF (các đỉnh lấy theo thứ tự đó và ngược chiều quay của kim đồng hồ) nội tiếp trong đường tròn tâm O. Tính số bằng rađian của các cung lượng giác: cung AB, AC, AD, AE, AF.
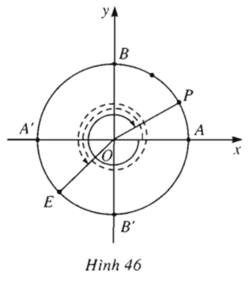
Tìm số đo của các góc lượng giác (OA, OE) và (OA, OP) trên hình 46 (điểm E là điểm chính giữa của cung(A'B'), sđ cung AP = 1/3 sđ cung AB). Viết số đo này theo đơn vị radian và theo đơn vị độ.
Cho tam giác ABC đường tròn nội tiếp tam giác tiếp xúc với các cạnh BC,CA , AB lần lượt tại các điểm M,N,P . các đoạn thẳng nối tâm đường tròn với các đỉnh cắt đường tròn lần lượt tại D,E,F.gọi I là iao điểm của MD và NE .CMR IP I
Bài 4 : ( 3,5 điểm)Cho tam giác ABC nhọn, vẽ đường tròn (O) đường kính BC cắt AB, AC lần lượt tại F và E. CF cắt BE tại H.
a) Chứng minh tứ giác AEHF nội tiếp
b) Gọi I là tâm đường tròn ngoại tiếp tứ giác AEHF, Tính số đo cung EHF, diện tích hình quạt IEHF của đường tròn (I) nếu góc BAC = 60o, AH = 4 cm.
c) AH giao BC tại D. Chứng minh FH là tia phân giác của góc DFE
d) Chứng minh 2 tiếp tuyến của (O) tại E, F và AH đồng quy tại 1 điểm
Khi biểu diễn trên đường tròn lượng giác các cung lượng giác nào trong các cung lượng giác có số đo dưới đây có cùng ngọn cung với cung lượng giác có số đo 42000
A.1300
B.1200
C.-1200
D.600
Cho tam giác ABC , AB> AC ngoại tiếp đường tròn (I ) và nội tiếp đường tròn (O). Đường tròn (I ) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi H là hình chiếu vuông góc của D trên EF. Đường tròn ngoại tiếp tam giác AEF cắt đường tròn (O) tại K (K khác A).
a) Chứng minh HD là phân giác của góc BHC .
b) Chứng minh ba điểm I, H, K thẳng hàng.
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = 80 o trong đó A(1; 0). Gọi M' là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM' là:
A. 170 o B. - 200 o
C. 190 o D. 280 o
Cho tam giác ABC nội tiếp đường tròn (O). P di chuyển trên cung B C ⏜ chứa A của (O).
I là tâm đường tròn nội tiếp tam giác ABC. Q là tâm đường tròn nội tiếp tam giác PBC.
1). Chứng minh rằng B, I, Q, C cùng nằm trên một đường tròn.
2) Trên tia BQ, CQ lần lượt lấy các điểm M, N sao cho B M = B I , C N = C I . Chứng minh rằng MN luôn đi qua một điểm cố định.
Cho tam giác ABC nhọn nội tiếp đường tròn (O). H là trực tâm của tam giác ABC.
AD là đường kính của (O). E thuộc AC sao cho HE//BC.
1). Chứng minh rằng các đường thẳng BH và DE cắt nhau trên (O)
2). Gọi F là giao điểm của các đường thẳng EH và AB. Chứng minh rằng A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Gọi I là tâm đường tròn nội tiếp của tam giác DEF. Chứng minh rằng BE, CF và IH đồng quy.
