\(\widehat{AB;A'C'}=\widehat{A'B';A'C'}=\widehat{B'A'C'}\)
Ta có: A'B'C'D' là hình vuông
=>A'C' là phân giác của góc B'A'D'
=>\(\widehat{B'A'C'}=\dfrac{1}{2}\cdot\widehat{B'A'D'}=45^0\)
=>\(\widehat{AB;A'C'}=45^0\)
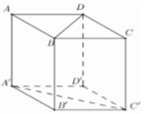
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và A’C’ là:
Cho hình lập phương ABCD.A’B’C’D’. Tính góc giữa các cặp đường thẳng sau đây:
a) AB và B’C’
b) AC và B’C’
c) A’C’ và B’C
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
Cho hình lập phương ABCD.A’B’C’D’ Góc giữa hai đường thẳng BA' và CD bằng:
A. 450
B.600
C. 300
D. 900
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng AC và C’D’ bằng:
A. 0 o
B. 45 o
C. 60 o
D. 90 o
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng
A. 90⁰.
B. 30⁰.
C. 60⁰.
D. 45⁰.
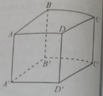
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a, gọi α là góc giữa đường thẳng AB’ và mặt phẳng (BB’D’D) Tính sin α
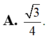
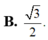
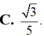
Cho hình lập phương ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của AA’ và CD. Góc giữa hai đường thẳng BM và C’N bằng:
A. 45 0
B. 30 0
C. 60 0
D. 90 0
Cho hình lập phương ABCD.A’B’C’D’. Hãy nêu tên các đường thẳng đi qua hai đỉnh của hình lập phương đã cho và vuông góc với:
a) đường thẳng AB
b) đường thẳng AC
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách giữa hai đường thẳng BD và CB’ bằng
A. a 6 3
B. 2 a 3 3
C. a 2 2
D. a 3 3
