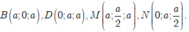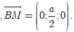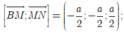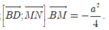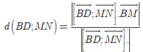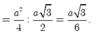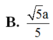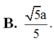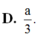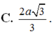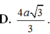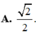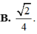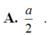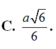Chọn D.
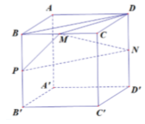
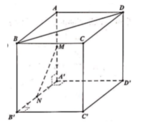
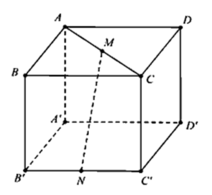
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN). Do đó:
d(MN;BD) = d(BD;(MPN)) = d(B;(MPN))
![]()
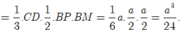
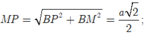
![]()
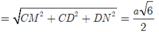
Nhận thấy ![]() nên tam giác MPN vuông tại M.
nên tam giác MPN vuông tại M.
Do đó 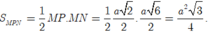
Ta có ![]()
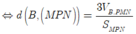

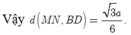
Cách 2:
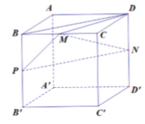
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN).
Đồng thời, MP//CB', PN//B'D' => (MPN)//(CB'D')
Do đó ![]()
![]()
(vì PC’ cắt B’C tại trọng tâm tam giác BB’C’).
Nhận thấy tứ diện C'.CB'D' là tứ diện vuông tại C' nên

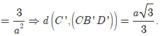
Vậy ![]()
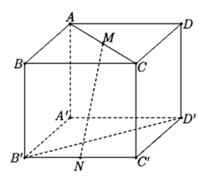
Cách 3: Tọa độ hóa
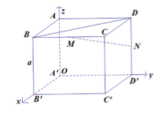
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó,