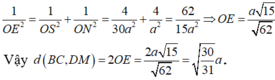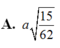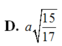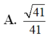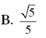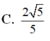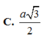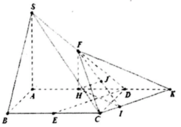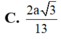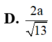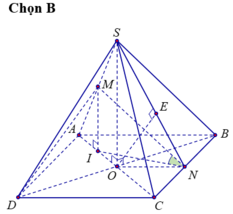
Gọi I là trung điểm OA. Vì IM// SO ⇒ IM⊥(ABCD) nên hình chiếu của MN lên (ABCD) là IN. Suy ra ![]()
Áp dụng định lí cô sin trong ΔCIN, ta có:
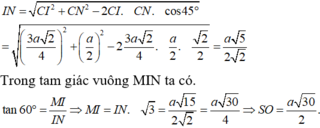
Ta có d(BC, DM) = d(BC, (SAD)) = d(N, (SAD)) = 2d(O, (SAD)) = 2d(O, (SBC)).
Kẻ OE ⊥ SN ⇒ OE ⊥ (SBC).
Ta có d(O, (SBC)) = OE mà