Các câu hỏi tương tự
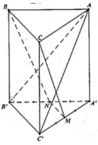
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có
A
B
2
3
và AA’2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng A.
6
13
65
B.
13
65
.
C.
17
13...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng
A. 6 13 65
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .
Cho hình lăng trụ tam giác đều
A
B
C
.
A
B
C
có
A
B
2
3
và
A
A
2
. Gọi M và N lần lượt là trung điểm của
A
C
và
A
B
. Tính cosin của góc tạo bởi hai mặt phẳng
A...
Đọc tiếp
Cho hình lăng trụ tam giác đều A B C . A ' B ' C ' có A B = 2 3 và A A ' = 2 . Gọi M và N lần lượt là trung điểm của A ' C ' và A ' B ' . Tính cosin của góc tạo bởi hai mặt phẳng A B ' C ' và (BCMN).
A. 13 65
B. - 13 65
C. 13 130
D. - 13 130
Cho hình lăng trụ tam giác đều ABC ABC có
A
B
2
3
và
A
A
2
. Gọi M và N lần lượt là trung điểm của AC và AB. Tính cosin của góc tạo bởi hai mặt phẳng
A
B
C
và
B
C
M
N
. A....
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC A'B'C' có A B = 2 3 và A A ' = 2 . Gọi M và N lần lượt là trung điểm của A'C' và A'B'. Tính cosin của góc tạo bởi hai mặt phẳng A B ' C ' và B C M N .
A. 13 65
B. − 13 65
C. 13 130
D. − 13 130
Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AB3; AC4và
A
A
61
2
Hình chiếu của B’ lên mặt phẳng (ABC) là trung điểm cạnh BC, điểm M là trung điểm A’B’ Tính cosin của góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) bằng: A.
11
3157
B.
13
65
C...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AB=3; AC=4và A A ' = 61 2 Hình chiếu của B’ lên mặt phẳng (ABC) là trung điểm cạnh BC, điểm M là trung điểm A’B’ Tính cosin của góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) bằng:
A. 11 3157
B. 13 65
C. 33 3517
D. 33 3157
Cho hình lăng trục tam giác ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AB 3, AC 4 và
A
A
61
2
. Hình chiếu của B’ lên mặt phẳng (ABC) là trung điểm của cạnh BC, M là trung điểm của cạnh A’B’. Cosin của góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) là A.
11...
Đọc tiếp
Cho hình lăng trục tam giác ABC.A’B’C’ có đáy là tam giác ABC vuông tại A, AB = 3, AC = 4 và A A ' = 61 2 . Hình chiếu của B’ lên mặt phẳng (ABC) là trung điểm của cạnh BC, M là trung điểm của cạnh A’B’. Cosin của góc tạo bởi hai mặt phẳng (AMC’) và (A’BC) là
A. 11 3157
B. 13 65
C. 33 3517
D. 33 3157
Cho hình lăng trụ tam giác đều ABC.ABC có
A
B
2
3
,
A
A
2
. Gọi M, N, P lần lượt là trung điểm của các cạnh AB,AC và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( ABC ) và ( MNP ) bằng A.
6
13
65
B.
13...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 , A A ' = 2 . Gọi M, N, P lần lượt là trung điểm của các cạnh A'B',A'C' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( AB'C' ) và ( MNP ) bằng

A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 13 65
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B’M
1
2
A’B’. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V1 và khối đa diện chứa đỉnh C’ có thể tích V2 . Tính
V
1
V
2...
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’. Trên A’B, kéo dài lấy điểm M sao cho B’M = 1 2 A’B’. Gọi N, P lần lượt là trung điểm của A’C’ và B’B. Mặt phẳng (MNP) chia khối lăng trụ ABC.A’B’C’ thành hai khối đa diện trong đó khối đa diện chứa đỉnh A’ có thể tích V1 và khối đa diện chứa đỉnh C’ có thể tích V2 . Tính V 1 V 2
A. V 1 V 2 = 97 59
B. V 1 V 2 = 49 144
C. V 1 V 2 = 95 144
D. V 1 V 2 = 49 95
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm H của A’B’. Gọi M, N lần lượt là trung điểm của AA’, B’C’. Biết rằng AH 2a và α là số đo của góc giữa đường thẳng MN và mặt phẳng (AC’H). Khi đó cosα bằng A.
77
11
B.
22
11
C.
2
5...
Đọc tiếp
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh 2a, hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm H của A’B’. Gọi M, N lần lượt là trung điểm của AA’, B’C’. Biết rằng AH = 2a và α là số đo của góc giữa đường thẳng MN và mặt phẳng (AC’H). Khi đó cosα bằng
A. 77 11
B. 22 11
C. 2 5 5
D. 5 5
Cho hình lăng trụ tam giác đều ABC.ABC có
A
B
2
3
và AA2. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC và BC. Côsin của góc tạo bởi hai mặt phẳng (ABC) và (MNP) bằng: A.
6
13
65
B.
13
65
C.
17...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 và AA'=2. Gọi M, N, P lần lượt là trung điểm của các cạnh A'B', A'C' và BC. Côsin của góc tạo bởi hai mặt phẳng (AB'C') và (MNP) bằng:
A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 63 65