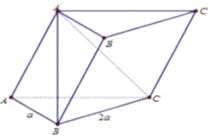
Cho hình lăng trụ ABC.A'B'C' ; đáy ABC có A C = a 3 ; B C = 3 a ; A C B ^ = 30 o . Cạnh bên hợp với mặt phẳng đáy góc 60 o và mặt phẳng (A'BC) vuông góc với (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A'AH) vuông góc với mặt phẳng A B C .Tính thể tích V của khối lăng trụ A'BC'D'
A. V = 4 a 3 9
B. V = 19 a 3 4
C. V = 9 a 3 4
D. V = 4 a 3 19
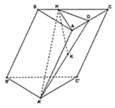
Áp dụng định lí côsin cho ∆ A H C ta dễ dàng tính được AH = a
Do
A ' B C ⊥ A B C A ' A H ⊥ A B C A ' H = A ' B C ∩ A ' A H ⇒ A ' H ⊥ A B C ⇒ A ' A H ^ = 60 o
Do ∆ A A ' H vuông tại H nên
A ' H = d A ' A B C = A H . tan 60 o = a 3
Vậy
V = S A B C . d A ' A B C = 1 2 . 3 a . a 3 sin 30 0 . a 3 = 9 a 3 4
Đáp án C