Đáp án B
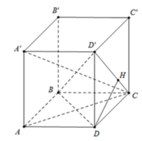
Tam giác A’AC vuông cân ⇒ A A ' = A C = A ' C 2 = a 2
Đáy ABCD là hình vuông nên A B = A D = A C 2 = a 2
Dựng D H ⊥ D ' C , lại có
B C ⊥ D C B C ⊥ D D ' ⇒ B C ⊥ D H S u y ra DH ⊥ B D ' C ⇒ d = D H = D C . D D ' C D 2 + D D ' 2 = a 6 6
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Đáp án B

Tam giác A’AC vuông cân ⇒ A A ' = A C = A ' C 2 = a 2
Đáy ABCD là hình vuông nên A B = A D = A C 2 = a 2
Dựng D H ⊥ D ' C , lại có
B C ⊥ D C B C ⊥ D D ' ⇒ B C ⊥ D H S u y ra DH ⊥ B D ' C ⇒ d = D H = D C . D D ' C D 2 + D D ' 2 = a 6 6
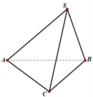
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , A B C ^ = 30 ° , tam giác SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách h từ điểm C đến mặt phẳng (SAB).
A. h = 2 a 39 13
B. h = a 39 13
C. h = a 39 26
D. h = a 39 52
Cho hình chóp S . A B C có đáy A B C là tam giác vuông tại B , A B = a , B C = a 3 . Hình chiếu vuông góc của S trên mặt đáy là trung điểm của cạnh A C .Biết S B = a 2 . Tính theo a khoảng cách từ H đến mặt phẳng S A B
A. 7 a 21 3
B. a 21 7
C. a 21 3
D. 3 a 21 7
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, A B = a , B C = a 3 . Tam giác SAC vuông S. Hình chiếu vuông góc của S xuống mặt phẳng đáy trùng với trung điểm H của đoạn AO. Khoảng cách từ điểm C đến mặt phẳng (SAB) theo a là
A. 2 a 15 5
B. a 15 10
C. 2 a 15 3
D. 8 a 15 3
Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 ° , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
A. h = 39 a 13
B. h = 2 15 a 5
C. h = 2 21 a 7
D. h = 15 a 5
Cho hình lăng trụ ABC.A’B’C’ có mặt đáy ABC là tam giác đều, độ dài cạnh AB =2a. Hình chiếu vuông góc của A’ lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 ° , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC’A’).
A. h = 39 a 13
B. h = 2 15 a 5
C. h = 2 21 a 7
D. h = 15 a 5
Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB = AC = a, I là trung điểm của SC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm H của BC, mặt phẳng (SAB) tạo với đáy 1 góc bằng 60 0 . Tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a .
A. 3 a 5
B. a 3 4
C. a 3 5
Cho hình lăng trụ đứng ABC.A' B' C' có đáy là tam giác vuông cân đỉnh A, BC=2a, thể tích khối lăng trụ đã cho bằng a 3 . Khoảng cách từ điểm B' đến mặt phẳng (A' BC) bằng
A. 2 a B. 6 a 4 . C. 2 a 2 . D. 6 a 3
B. 6 a 4 .
C. 2 a 2 .
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B có AB=2a, SB=3a Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm H của AB. Tính khoảng cách d từ điểm H đến MP (SBC).
A. d = a 2 3
B. d = 2 a 2 3
C. d = 4 a 2 3
D. d = a 2
Cho hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình vuông cạnh a.
Khoảng cách từ điểm A đến mặt phẳng
(A'BCD') bằng a 3 2 . Tính thể tích hình hộp theo a.
A. V = a 3 3 3
B. V = a 3 3
C. V = a 3 21 7
D. V = a 3