Đáp án B.
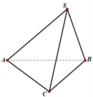
Gọi H là trung điểm của BC khi đó S H ⊥ B C do S B C ⊥ A B C ⇒ S H ⊥ A B C
Lại có: C B = 2 C H ⇒ d C ; S A B = 2 d H ; S A B
Dựng H E ⊥ A B H F ⊥ S E ⇒ d H = H F
Mặt khác H E = A C 2 = 1 2 B C . sin A B C ^ = a 4 ; S H = a 3 2
Do đó H F = S H . H E S H 2 + H E 2 = a 39 26 ⇒ d c = a 39 13