Chọn C.
Phương pháp:
+) Thể tích khối tứ diện OABC có OA, OB, OC đôi một vuông góc và có độ dài các cạnh đó lần lượt là a, b, c là: V = 1 6 a b c
Cách giải:
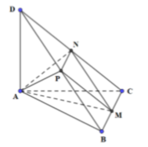
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau AB=3, AC=4, AD=5. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP
A. 5 2
B. 8 3
C. 20 7
D. 15 6
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau A B = 3 , A C = 4 , A D = 5 . Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Tính thể tích tứ diện AMNP.
A. 15 6
B. 20 7
C. 8 3
D. 5 2
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau; A B = 6 a ; A C = 7 a và A D = 4 a . Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích V của tứ diện AMNP
A. V = 7 2 a 3
B. V = 7 a 3
C. V = 28 3 a 3
D. V = 14 a 3
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng A B = a , A C = a 2 , A D = a 3 , a > 0 . Thể tích V của khối tứ diện ABCD là:
A. V = 1 3 a 3 6
B. V = 1 6 a 3 6
C. V = 1 2 a 3 6
D. V = 1 9 a 3 6
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, A B = 6 a , A C = 7 a , A D = 8 a . . Gọi M, N, P lần lượt là trung điểm của BC, CD, BD Thể tích khối tứ diện AMNP là:
A. 14 a 2
B. 28 a 2
C. 42 a 2
D. 7 a 2
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho tứ diện ABCD có các cạnh AB,AC,AD vuông góc với nhau từng đôi một và AB=3a,AC=6a,AD=4a. Gọi M,N,P lần lượt là trung điểm các cạnh BC,CD,BD . Tính thể tích khối đa diện AMNP
A. 3 a 3
B. 12 a 3
C. a 3
D. 2 a 3
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
