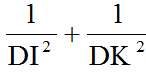Áp dụng hệ thức lượng trong tam giác vuông vào ΔADC vuông tại D có DE là đường cao ứng với cạnh huyền AC, ta được:
\(\dfrac{1}{DE^2}=\dfrac{1}{AD^2}+\dfrac{1}{DC^2}\)
\(\Leftrightarrow\dfrac{1}{DE^2}=\dfrac{1}{6^2}+\dfrac{1}{32^2}=\dfrac{265}{9216}\)
hay \(DE=\dfrac{96\sqrt{265}}{265}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔDEA vuông tại E, ta được:
\(DE^2+EA^2=DA^2\)
\(\Leftrightarrow EA^2=32^2-\left(\dfrac{96\sqrt{265}}{265}\right)^2=\dfrac{262144}{265}\)
hay \(EA=\dfrac{512\sqrt{265}}{265}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDAC vuông tại D có DE là đường cao ứng với cạnh huyền AC, ta được:
\(ED^2=EA\cdot EC\)
\(\Leftrightarrow EC=\dfrac{9216}{265}\cdot\dfrac{265}{512\sqrt{265}}\)
hay \(EC=\dfrac{18\sqrt{265}}{265}\left(cm\right)\)