Đáp án C
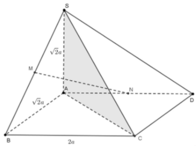
Kẻ C N ⊥ A B , ta dễ dàng tính được
B D = 5 a ; C D = 2 a ; A C = 2 a ; A C 2 + D C 2 = A D 2 ⇒ � A D C
vuông tại C, Từ đó N C ⊥ S A C , Gọi O là trung điểm của AC, dễ dàng cm được B D ⊥ S A C ⇒ M K ⊥ S A C . vơí K là trung điểm của SO, từ đó KC là hc của MN lên SAC .
Ta kẻ K Z ⊥ A C ⇒ C K = C Z 2 + K Z 2 = 22 4 a .
M N = M T 2 + T N 2 = 10 2 a với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC) ⇒ cos α = C K M N = 55 10