Đáp án là C.
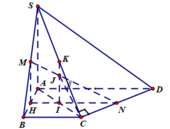

Ta dễ chứng minh được tam giácACD vuông tại C, từ đó chứng minh được CN vuông góc với mặt phẳng (SAC) hay C là hình chiếu vuông góc của N trên (SAC). Đường thẳng MN cắt mặt phẳng (SAC) tại J xác định như hình vẽ. Suy ra góc giữa MN và (SAC) là góc NJC .
IN là đương trung bình trong tam giác ACD suy ra IN=a, IH là đường trung bình trong tam giác ABC suy ra I H = 1 2 B C = a 2 . Dựa vào định lí Talet trong tam giác MHN ta được I J = 2 3 M H = 2 3 . 1 2 S A = 1 3 S A = a 3 . Dựa vào tam giác JIC vuông tại I tính được J C = 22 6 .
Ta dễ tính được C N = a 2 2 , J N = a 10 3 .
Tam giác NJC vuông tại C nên cos N J C ^ = J C J N = 55 10 .

