Question

cho hình chóp S.ABCD, đáy ABCD là vuông, tâm I. Gọi M là trung điểm SA

a) vẽ hình

b) chứng minh CD ∥ (SAB)

c) chứng minh AD ∥ (SBC)

d) chứng minh IM ∥ (SCD)

Answer 1

a: 

b: CD//AB(ABCD là hình vuông)

\(AB\subset\left(SAB\right)\)

CD không nằm trong(SAB)

Do đó: CD//(SAB)

c: AD//BC(ABCD là hình vuông)

\(BC\subset\left(SBC\right)\)

AD không nằm trong mp(SBC)

Do đó: AD//(SBC)

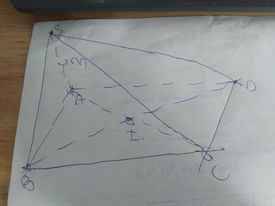
d: Xét ΔSAC có

M,I lần lượt là trung điểm của AS,AC

=>MI là đường trung bình của ΔSAC

=>MI//SC

mà \(SC\subset\left(SCD\right)\) và \(IM\) không nằm trong mp(SCD)

nên IM//(SCD)