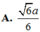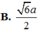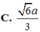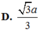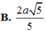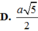Cho I là trung điểm AD, O là giao AC và BI
Ta có SA vuông BI ; AC vuông BI (AICB là hình vuông) ; SA; AC thuộc (SAC)
=> BI vuông (SAC) => BO vuông (SAC) => BO vuông SC
Từ O kẻ OH vuông SC
Lại có OH vuông SC, BO vuông SC ; BO; OH thuộc (BOH)
=> SC vuông (BOH)
=> d(B;SC) = BH
Mặt khác SA vuông BC; AB vuông BC; SA;AB thuộc (SAB)
=> BC vuông (SAB) => BC vuông SB
=> tam giác SBC vuông tại B
Xét tam giác SAB vuông tại A
Theo Pytago ta có \(SB=\sqrt{SA^2+AB^2}=\sqrt{3a^2+a^2}=2a\)
Xét tam giác SBC vuông tại B, đường cao BH
ADHT \(\dfrac{1}{BH^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}=\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BH=\dfrac{2a}{\sqrt{5}}\)