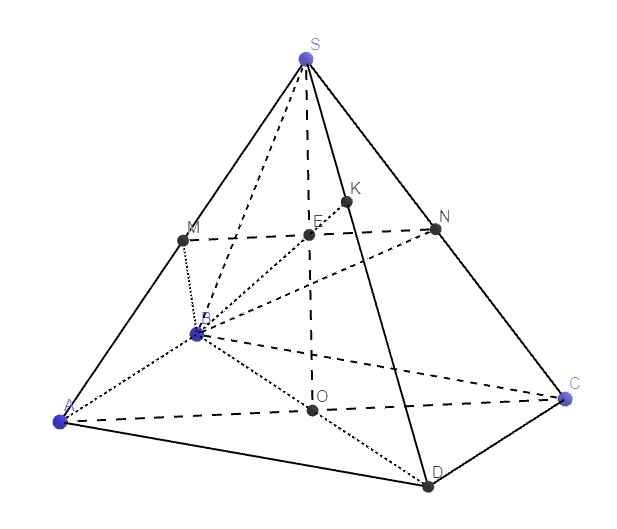
Gọi O là tâm đáy \(\Rightarrow SO=\left(SBD\right)\cap\left(SAC\right)\)
Trong mp (SAC), gọi E là giao điểm SO và MN
MN là đường trung bình tam giác SAC \(\Rightarrow\) E là trung điểm SO
Trong mp (SAD), nối BE kéo dài cắt SD tại K
\(\Rightarrow K=SD\cap\left(BMN\right)\)
Áp dụng định lý Menelaus cho tam giác SOD:
\(\dfrac{ES}{EO}.\dfrac{BO}{BD}.\dfrac{KD}{KS}=1\Rightarrow1.\dfrac{1}{2}.\dfrac{KD}{SK}=1\Rightarrow KD=2SK\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}\)