Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Trong mặt phẳng đáy vẽ đường thẳng d đi qua A và không song song với các cạnh hình bình hành, d cắt đoạn BC tại E. Gọi C' là một điểm nằm trên cạnh SC.
a) Tìm giao điểm M của CD và mặt phẳng (C'AE)
b) Tìm thiết diện của hình chóp cắt bởi mặt phẳng (C'AE)
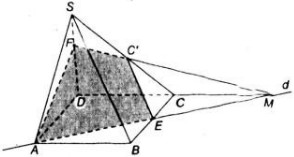
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE).
b)
Do M = DC ∩ (C'AE) nên M ∈ (SDC),.
Trong (SDC) : MC' ∩ SD = F.
Ta có:
\(\left(C'AE\right)\cap\left(SDC\right)=FC'\)
\(\left(C'AE\right)\cap\left(SAD\right)=AF\)
\(\left(C'AE\right)\cap\left(ABCD\right)=AE\)
\(\left(C'AE\right)\cap\left(SBC\right)=C'E\)
Vậy thiết diện là AEC'F.
Đúng 0
Bình luận (0)