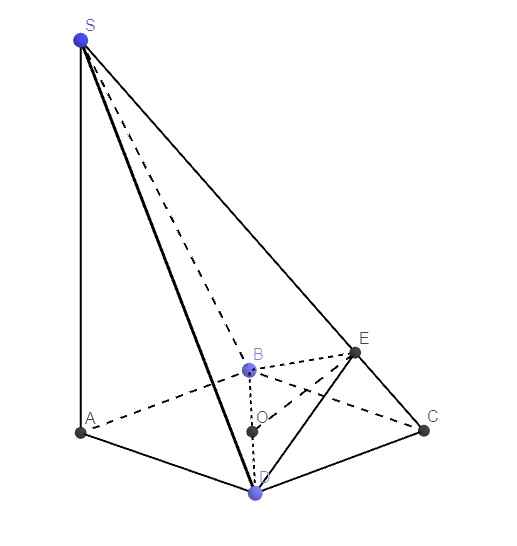
\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)