\(SA\perp ABCD\Rightarrow SA\) vuông góc với các đường thẳng AB, BC, CD, DA, AC, BD
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy, SA AB a. Tính góc giữa đường thẳng SC và mặt phẳng . A. arcsin
1
4
B. arcsin
1
3
C. arcsin
1
3
D. arcsin
2
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a. Tính góc giữa đường thẳng SC và mặt phẳng .
A. arcsin 1 4
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy, SA AB a Tính góc giữa đường thẳng SC và mặt phẳng (SBD) A. arcsin
1
4
B. arcsin
1
3
C. arcsin
1
3
D. arcsin
2
3
B. arcsin
1
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bên SA vuông góc với mặt phẳng đáy, SA = AB = a Tính góc giữa đường thẳng SC và mặt phẳng (SBD)
A. arcsin 1 4 B. arcsin 1 3 C. arcsin 1 3 D. arcsin 2 3
B. arcsin 1 3
C. arcsin 1 3
D. arcsin 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 2 . Chứng minh rằng các mặt bên hình chóp là những tam giác vuông.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA
a
3
. Tính thể tích V của khối chóp S.ABCD. A.
V
3
a
3
B.
V
3
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA= a 3 . Tính thể tích V của khối chóp S.ABCD.
A. V = 3 a 3
B. V = 3 a 3 3
C. V = a 3
D. V = a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và SA
a
2
Tính thể tích V của khối chóp S.ABCD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và SA= a 2 Tính thể tích V của khối chóp S.ABCD
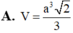
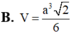
![]()
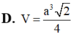
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC
a
5
. Tính thể tích khối chóp.
A
.
V
a
3
3
3
B
.
V
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy (ABCD), SC = a 5 . Tính thể tích khối chóp.
A . V = a 3 3 3
B . V = a 3 3 6
C . V = a 3 3
D . V = a 3 3 9
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA a
3
vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a, SA = a 3 vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) bằng:
![]()
![]()
![]()
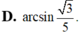
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với ABa, BCa
3
Cạnh bên SA a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng A.
3
2
B.
14
4
C.
3
5...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, BC=a 3 Cạnh bên SA =a và vuông góc với đáy (ABCD) Cosin của góc tạo bởi giữa đường thẳng BD và mặt phẳng (SBC) bằng
A. 3 2
B. 14 4
C. 3 5
D. 22 5
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SAa và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng A.
a
3
4
B.
a
6
3
C.
a
2
D.
a
6
6
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA=a và vuông góc với mặt đáy (ABCD). Khoảng cách giữa hai đường thẳng SC và BD bằng
A. a 3 4
B. a 6 3
C. a 2
D. a 6 6
