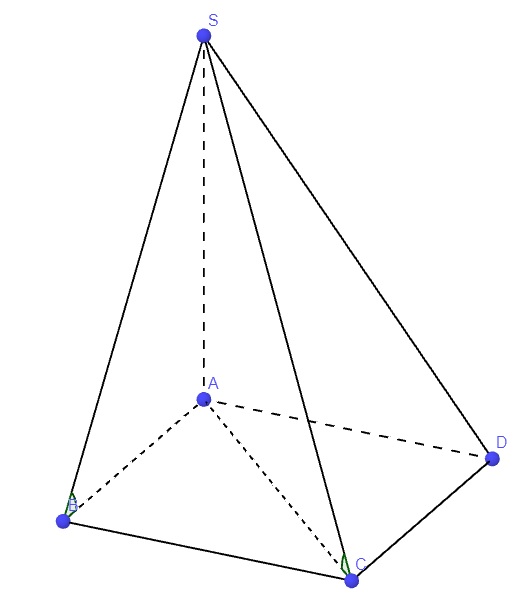
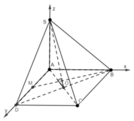
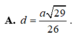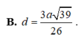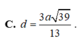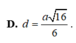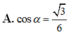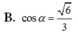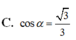Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. SA vuông góc với mặt phẳng đáy SA = a căn 2. Chứng minh: xác định góc giữa đường thẳng SC và mặt phẳng ABCD
a) Cm : BC vuông góc (SBD)
b) Cm: (SAC) vuông góc với (SBC)
c). Tính khoảng cách từ đường thẳng A và (SBC)
d). Xác định và tính góc giữa đường thẳng SC và (ABCD)
e). Xác định và tính góc giữa (SBC) và (ABCD)
f). Tính VsABC
(Mọi người sửa giùm em câu d, e và f thôi cũng được ạ)
d.
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=a\sqrt{2}\) (đường chéo hình vuông)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{2}}{a\sqrt{2}}=1\)
\(\Rightarrow\widehat{SCA}=45^0\)
e.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{2}}{a}=\sqrt{2}\)
\(\Rightarrow\widehat{SBA}\approx54^044'\)
f. Đúng là \(V_{S.ABC}\) chứ ko phải \(V_{S.ABCD}\) phải ko em?
\(V_{S.ABC}=\dfrac{1}{3}.SA.\dfrac{1}{2}AB.BC=\dfrac{1}{3}.a\sqrt{2}.\dfrac{1}{2}a^2=\dfrac{a^3\sqrt{2}}{6}\)