Vì ABCD là hình vuông nên OA = OB = OC (1)
Dễ dàng chứng minh được A H ⊥ H C nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC
Từ (1) và (2) suy ra ![]()
Vì ABCD là hình vuông nên OA = OB = OC (1)
Dễ dàng chứng minh được A H ⊥ H C nên tam giác AHC vuông tại H và có O là trung điểm cạnh huyền AC nên suy ra OH = OC
Từ (1) và (2) suy ra ![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và B D = a . Hình chiếu vuông góc của S trên mặt phẳng đáy là trung điểm OD. Đường thẳng SD tạo với mặt đáy một góc bằng 60 ° . Bán kính mặt cầu ngoại tiếp hình chóp S.ABCD bằng
A. a
B. a 2
C. a 3
B. a 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy SA = a 2 . Gọi M, N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB, SD (tham khảo hình vẽ). Góc giữa mặt phẳng (AMN) và đường thẳng SB bằng
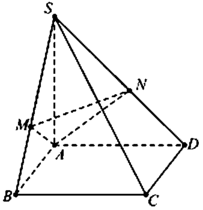
A. 45 °
B. 60 °
C. 90 °
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc A B C ^ = 60 ° , cạnh bên SA=a và vuông góc với mặt đáy. Tính bán kính R của mặt cầu ngoại tiếp tứ diện S.ACD
A. R = a 5 2
B. R = a
C. R = a 7 12
D. R = a 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông có cạnh bằng a, cạnh bên SA vuông góc với mặt phẳng đáy và SA=a.Gọi H, K lần lượt là hình chiếu vuông góc của A trên SB, SD (tham khảo hình vẽ bên). Tang của góc tạo bởi đường thẳng SD và mặt phẳng (AHK) bằng
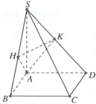
A. 3
B. 2
C. 1 3
D. 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với 𝐴𝐵=𝐴𝐷=1, 𝐶𝐷=2. Cạnh bên SD vuông góc với mặt đáy, còn cạnh bên SA tạo với mặt đáy một góc 45°. Gọi E là trung điểm của cạnh CD. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.BCE.
A. R = 3 2
B. R = 14 2
C. R = 5 2
D. R = 11 2
Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy S A = a 2 . Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp S.AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Cho hình chóp S.ABCD có SA vuông góc với đáy; S A = a 6 . Đáy ABCD là hình thang vuông tại A và B, A B = B C = 1 2 A D = a . Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD
A. R = a 30 3
B. R = a 19 6
C. R = a 6
D. R = 114 6 a .
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Gọi M, N lần lượt là trung điểm của SB và SD. Biết AM vuông góc với CN. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 2 a 10 .
B. 3 a 10 .
C. a 10 .
D. 4 a 10 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA=2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM)
A. d = 3 a 2 .
B. d = a .
C. d = 2 a 3 .
D. d = a 3 .