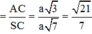Đáp án B
Phương pháp:
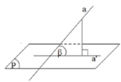
- Cách xác định góc giữa hai mặt phẳng:
Gọi a’ là hình chiếu vuông góc của a trên mặt phẳng (P).
Góc giữa đường thẳng a và mặt phẳng (P) là góc giữa đường thẳng a và a’.
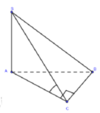
Cách giải: Tam giác ABC vuông tại C có AB = 2a; C A B ^ = 30 0
![]()
![]()
Tam giác SAC vuông tại A
![]()
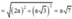
Vì SA ⊥ (ABC) => (SC;(ABC)) = (SC;AC) = S C A ^
![]()