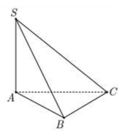
Phương pháp:
+) Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC. Chứng minh ∠ S A ; B C = ∠ N Q ; M Q
+) Áp dụng định lí cosin trong tam giác MNQ.
Cách giải:
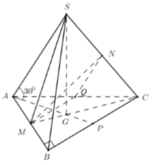


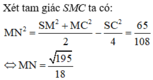
Áp dụng định lý cosin trong tam giác MNQ:
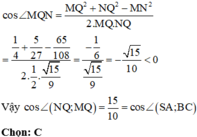
Chú ý: Góc giữa hai đường thẳng là góc nhọn nên cosin của góc giữa hai đường thẳng là giá trị dương.