Cho hình chóp S.ABC có S A ⊥ A B C và Δ A B C vuông tại C. Gọi O là tâm đường tròn ngoại tiếp tam giác S B C . H là hình chiếu vuông góc của O lên (ABC). Khẳng định nào sau đây đúng?
A. H là tâm đường tròn nội tiếp tam giác Δ A B C
B. H là trọng tâm tam giác Δ A B C
C. H là trung điểm cạnh AB
D. H là trung điểm cạnh AC
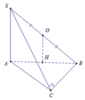
Đáp án C
Do B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ S A C ⇒ B C ⊥ S C
Do đó O là trung điểm của SB. Do đó H là hình chiếu vuông góc của O lên m p A B C ⇒ H là trung điểm của AB

