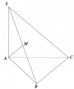
Đáp án B.
Gọi F là trung điểm của B D ⇒ E F / / C D
Góc giữa SE và CD là góc giữa SE và EF.
Ta có C D = 2 2 . 3 2 = 6 ⇒ E F = 6 2
Lại có S E = S C 2 + C E 2 = 1 2 + 2 2 = 3
Trong tam giác vuông C D F : C F = C D 2 + D F 2 = 6 2 + 2 2 4 2 = 13 2
Trong tam giác vuông S C F :
S F = S C 2 + C F 2 = 1 2 + 13 2 2 = 15 2
Trong tam giác S E F :
cos S E F ^ = S E 2 + E F 2 − S F 2 2 S E . E F = 3 + 6 4 − 15 2 2 3 . 6 2 = − 2 2
⇒ S E F ^ = 3 π 4 ⇒ Góc giữa SE và CD bằng π − 3 π 4 = π 4 .
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2 2 , cạnh SC vuông góc với đáy và SC=1. Gọi D và E lần lượt là trung điểm của AB và BC. Tính góc giữa hai đường thẳng CD và SE.
A. 3 π 4
B. π 4
C. 2 π 3
D. π 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều, cạnh a, SA vuông góc với mặt đáy và SA = 3a. Gọi M, N lần lượt là trung điểm của AB, SC. Khoảng cách giữa hai đường thẳng CM và AN bằng
A. 3 a 37 .
B. a 2 .
C. 3 a 37 74 .
D. a 4 .
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a = 4 2 c m , cạnh bên SC vuông góc với đáy và SC=2cm. Gọi M,N là trung điểm của AB và BC. Góc giữa hai đường thẳng SN và CM là
A. 45 0 .
B. 30 0 .
C. 60 0 .
D. 90 0 .
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SA= 3 a và vuông góc với mặt đáy. Gọi M là trung điểm cạnh SB (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng AM và SC bằng
A. 5 16
B. 11 16
C. 5 8
D. 3 8
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B , A B = 3 a , B C = 4 a . Cạnh bên SA vuông góc với đáy. Góc tạo bởi giữa SC với đáy bằng 60 ° . Gọi M là trung điểm AC, tính khoảng cách giữa hai đường thẳng AB và SM
A. a 3
B. 10 a 3 79
C. 5 a 2
D. 5 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B ; A B = 3 a ; B C = 4 a . Cạnh bên SA vuông góc với mặt phẳng đáy. Góc tạo giữa SC và mặt phẳng đáy bằng 60 ° . Gọi M là trung điểm của AC. Khoảng cách giữa hai đường thẳng AB và SM bằng
A. a 3
B. 10 a 3 79
C. 5 a 3
D. 5 a 2
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho HA=2HB. Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H thuộc cạnh AB sao cho H A = 2 H B . Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng 60°. Tính khoảng cách d giữa hai đường thẳng SA và BC theo a.
A. d = a 42 8
B. d = a 21 12
C. d = a 42 12
D. d = a 462 66
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và SA=2a. Gọi M là trung điểm của SC. Tính côsin của góc α là góc giữa đường thẳng BM và mặt phẳng (ABC).
A. cos α = 7 14
B. cos α = 2 7 7
C. cos α = 5 7
D. cos α = 21 7
