Đáp án B
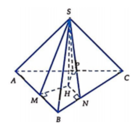
Gọi H là chân đường vuông góc hạ từ S xuống mặt phẳng (ABC).
Kẻ HM, HN, HP lần lượt vuông góc với AB, BC, CA trong mặt phẳng (ABC).
Sử dụng tính chất ba đường cvuoong góc ta dễ chứng minh được SM, SN, SP lần lượt vuông góc với AB, BC, CA. Từ đây suy ra S M H ^ , S N H ^ , S P H ^ là các gốc tạo bởi mặt bên và mặt đáy (ABC). Do đó S M H ^ = S N H ^ = S P H ^ = 60 0 .
Suy ra H M = H N = H P = S H . cot 60 0 nên H là tâm đường tròn nội tiếp tam giác ABC.
Sử dụng công thức Hê rông ta tính được S A B C = 6 6 a 2
Và ta tính được bán kính đường trọn nội tiếp r = S p = 6 6 a 2 9 a = 2 6 a 3
Ta cũng có S H = r . tan 60 0 = 2 6 a 3 . 3 = 2 2 a
Vậy V S A B C = 1 3 . S H . S A B C = 1 3 .2 2 a .6 6 a 2 = 8 3 a 3

