Đáp án D
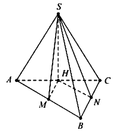
Gọi H là hình chiếu của S trên A C ⇒ S H ⊥ A B C
Kẻ H M ⊥ A B M ∈ A B , H N ⊥ A C N ∈ A C
Suy ra S A B ; A B C ^ = S B C ; A B C ^ = S M H ^ = S N H ^ = 60 °
⇒ ∆ S H M = ∆ S H N ⇒ H M = H N ⇒ H là trung điểm của AC
Tam giác SHM vuông tại H, có tan S M H ^ = S H H M ⇒ S H = a 3 2
Diện tích tam giác ABC là S ∆ A B C = 1 2 . A B . B C = a 2 2
Vậy thể tích cần tính là V = 1 3 . S H . S A B C = 1 3 . a 3 2 . a 2 2 = a 3 3 12

